0%

Datawhale零基础入门数据挖掘-Task1

发表于 更新于 分类于 阅读次数：
本文字数： 6.5k 阅读时长 ≈ 6 分钟

  • 学习背景:由Datawhale与天池开放的零基础入门数据挖掘赛事-二手车交易价格预测

  • 赛题概括:赛题以预测二手车的交易价格为任务，数据集报名后可见并可下载，该数据来自某交易平台的二手车交易记录，总数据量超过40w，包含31列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取15万条作为训练集，5万条作为测试集A，5万条作为测试集B，同时会对name、model、brand和regionCode等信息进行脱敏。

赛题分析

数据概括

一般而言，对于数据在比赛界面都有对应的数据概况介绍（匿名特征除外），说明列的性质特征。了解列的性质会有助于我们对于数据的理解和后续分析。 Tip:匿名特征，就是未告知数据列所属的性质的特征列。

train.csv

  • SaleID - 销售样本ID
  • name - 汽车编码
  • regDate - 汽车注册时间
  • model - 车型编码
  • brand - 品牌
  • bodyType - 车身类型
  • fuelType - 燃油类型
  • gearbox - 变速箱
  • power - 汽车功率
  • kilometer - 汽车行驶公里
  • notRepairedDamage - 汽车有尚未修复的损坏
  • regionCode - 看车地区编码
  • seller - 销售方
  • offerType - 报价类型
  • creatDate - 广告发布时间
  • price - 汽车价格
  • ‘v_0’, ‘v_1’, ‘v_2’, ‘v_3’, ‘v_4’, ‘v_5’, ‘v_6’, ‘v_7’, ‘v_8’, ‘v_9’, ‘v_10’, ‘v_11’, ‘v_12’, ‘v_13’,’v_14’ 【匿名特征，包含v0-14在内15个匿名特征】 　

评测标准

赛题评价目标为MAE(Mean Absolute Error):


MAE越小，说明模型预测得越准确

预测建模

  • 预测建模就是使用历史数据建立一个模型，去给没有答案的新数据做预测的问题

关于预测建模，可以在下面这篇文章中了解更多信息:

Gentle Introduction to Predictive Modeling: https://machinelearningmastery.com/gentle-introduction-to-predictive-modeling/

预测建模可以被描述成一个近似求取从输入变量（X）到输出变量（y）的映射函数的数学问题。这被称为函数逼近问题

建模算法的任务就是在给定的可用时间和资源的限制下，去寻找最佳映射函数。更多关于机器学习中应用逼近函数的内容，请参阅下面这篇文章：

机器学习是如何运行的（how machine learning work,https://machinelearningmastery.com/how-machine-learning-algorithms-work/)

一般而言，我们可以将函数逼近任务划分为分类任务和回归任务

分类预测建模

分类预测建模是逼近一个从输入变量（X）到离散的输出变量（y）之间的映射函数（f）

输出变量经常被称作标签或者类别。映射函数会对一个给定的观察样本预测一个类别标签

例如，一个文本邮件可以被归为两类：「垃圾邮件」，和「非垃圾邮件」

  • 分类问题需要把样本分为两类或者多类
  • 分类的输入可以是实数也可以有离散变量
  • 只有两个类别的分类问题经常被称作两类问题或者二元分类问题
  • 具有多于两类的问题经常被称作多分类问题
  • 样本属于多个类别的问题被称作多标签分类问题

分类模型经常为输入样本预测得到与每一类别对应的像概率一样的连续值。这些概率可以被解释为样本属于每个类别的似然度或者置信度。预测到的概率可以通过选择概率最高的类别转换成类别标签

例如，某封邮件可能以 0.1 的概率被分为「垃圾邮件」，以 0.9 的概率被分为「非垃圾邮件」。因为非垃圾邮件的标签的概率最大，所以我们可以将概率转换成「非垃圾邮件」的标签

有很多用来衡量分类预测模型的性能的指标，但是分类准确率可能是最常用的一个

例如，如果一个分类预测模型做了 5 个预测，其中有 3 个是正确的，2 个这是错误的，那么这个模型的准确率就是 60%：

accuracy = correct predictions / total predictions * 100
accuracy = 3 / 5 * 100
accuracy = 60%

能够学习分类模型的算法就叫做分类算法

回归预测模型

回归预测建模是逼近一个从输入变量（X）到连续的输出变量（y）的函数映射

连续输出变量是一个实数，例如一个整数或者浮点数。这些变量通常是数量或者尺寸大小等等

例如，一座房子可能被预测到以 xx 美元出售，也许会在 $100,000 t 到$200,000 的范围内

  • 回归问题需要预测一个数量
  • 回归的输入变量可以是连续的也可以是离散的
  • 有多个输入变量的通常被称作多变量回归
  • 输入变量是按照时间顺序的回归称为时间序列预测问题
  • 因为回归预测问题预测的是一个数量，所以模型的性能可以用预测结果中的错误来评价

有很多评价回归预测模型的方式，但是最常用的一个可能是计算误差值的均方根，即 RMSE

例如，如果回归预测模型做出了两个预测结果，一个是 1.5，对应的期望结果是 1.0；另一个是 3.3 对应的期望结果是 3.0. 那么，这两个回归预测的 RMSE 如下：

RMSE = sqrt(average(error^2))
RMSE = sqrt(((1.0 - 1.5)^2 + (3.0 - 3.3)^2) / 2)
RMSE = sqrt((0.25 + 0.09) / 2)
RMSE = sqrt(0.17)
RMSE = 0.412

使用 RMSE 的好处就是错误评分的单位与预测结果是一样的

一个能够学习回归预测模型的算法称作回归算法

有些算法的名字也有「regression,回归」一词，例如线性回归和 logistics 回归，这种情况有时候会让人迷惑因为线性回归确实是一个回归问题，但是 logistics 回归却是一个分类问题

分类 vs 回归

分类预测建模问题与回归预测建模问题是不一样的

  • 分类是预测一个离散标签的任务
  • 回归是预测一个连续数量的任务

分类和回归也有一些相同的地方：

  • 分类算法可能预测到一个连续的值，但是这些连续值对应的是一个类别的概率的形式
  • 回归算法可以预测离散值，但是以整型量的形式预测离散值的

有些算法既可以用来分类，也可以稍作修改就用来做回归问题，例如决策树和人工神经网络。但是一些算法就不行了——或者说是不太容易用于这两种类型的问题，例如线性回归是用来做回归预测建模的，logistics 回归是用来做分类预测建模的

重要的是，我们评价分类模型和预测模型的方式是不一样的，例如：

  • 分类预测可以使用准确率来评价，而回归问题则不能
  • 回归预测可以使用均方根误差来评价，但是分类问题则不能

分类问题和回归问题之间的转换

在一些情况中是可以将回归问题转换成分类问题的。例如，被预测的数量是可以被转换成离散数值的范围的

例如，在$0 到$100 之间的金额可以被分为两个区间：

  • class 0：$0 到$49
  • class 1: $50 到$100

这通常被称作离散化，结果中的输出变量是一个分类，分类的标签是有顺序的（称为叙序数）

在一些情况中，分类是可以转换成回归问题的。例如，一个标签可以被转换成一个连续的范围

一些算法早已通过为每一个类别预测一个概率，这个概率反过来又可以被扩展到一个特定的数值范围：

quantity = min + probability * range

与此对应，一个类别值也可以被序数化，并且映射到一个连续的范围中：

  • $0 到 $49 是类别 1
  • $0 到 $49 是类别 2

如果分类问题中的类别标签没有自然顺序的关系，那么从分类问题到回归问题的转换也许会导致奇怪的结果或者很差的性能，因为模型可能学到一个并不存在于从输入到连续输出之间的映射函数

原文链接https://machinelearningmastery.com/classification-versus-regression-in-machine-learning/

关于评价指标

  • 评估指标即是我们对于一个模型效果的数值型量化。（有点类似与对于一个商品评价打分，而这是针对于模型效果和理想效果之间的一个打分）

一般来说分类和回归问题的评价指标有如下一些形式：

分类算法常见的评估指标如下：

  • 对于二类分类器/分类算法，评价指标主要有accuracy， Precision，Recall，F-score，Pr曲线，ROC-AUC曲线
  • 对于多类分类器/分类算法，评价指标主要有accuracy， 宏平均和微平均，F-score

对于回归预测类常见的评估指标如下:

  • 平均绝对误差（Mean Absolute Error，MAE），均方误差（Mean Squared Error，MSE），平均绝对百分误差（Mean Absolute Percentage Error，MAPE），均方根误差（Root Mean Squared Error）， R2（R-Square）

平均绝对误差

  • 平均绝对误差（Mean Absolute Error，MAE）:其能更好地反映预测值与真实值误差的实际情况，其计算公式如下：
    $$MAE=\frac{1}{N} \sum_{i=1}^{N}\left|y_{i}-\hat{y}_{i}\right|$$

均方误差

  • 均方误差（Mean Squared Error，MSE）,均方误差,其计算公式为：
    $$MSE=\frac{1}{N} \sum_{i}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}$$

R2（R-Square）

  • 残差平方和:
    $$SS_{res}=\sum\left(y_{i}-\hat{y}_{i}\right)^{2}$$
  • 总平均值:
    $$SS_{tot}=\sum\left(y_{i}-\overline{y}_{i}\right)^{2}$$
  • 其中$\overline{y}$表示$y$的平均值得到$R^2$的表达式为:

$$R^{2}=1-\frac{SS_{res}}{SS_{tot}}$$

$R^2$用于度量因变量的变异中可由自变量解释部分所占的比例，取值范围是 0~1，$R^2$越接近1,表明回归平方和占总平方和的比例越大,回归线与各观测点越接近，用x的变化来解释y值变化的部分就越多,回归的拟合程度就越好。所以$R^2$也称为拟合优度（Goodness of Fit）的统计量

$y_{i}$表示真实值,

$\hat{y}_{i}$表示预测值,

$\overline{y}_{i}$表示样本均值。得分越高拟合效果越好

几何解释


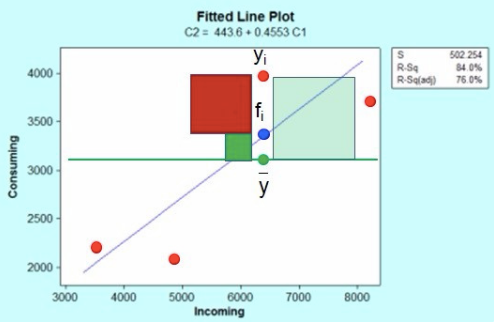
上图红色点是incoming自变量与Consuming因变量对应的散点图，蓝色线是回归方程线（最小二乘法得到）；
这里红色点$y_{i}$表示一个响应观测值点（共4个），蓝色点$f_{i}$是响应观测值对应的回归曲线上的点，两个的差值就是残差，残差值共有4个,$\overline{y}$是响应变量的平均值。

根据平方和分解公式: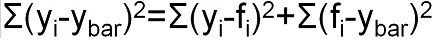

即：SS 总体=SS 回归 + SS 残差 (观测值与平均值的差值平方和被残差平方和以及回归差值平方和之和解释)

分析结果

  1. 此题为传统的数据挖掘问题，通过数据科学以及机器学习深度学习的办法来进行建模得到结果。
  2. 此题是一个典型的回归问题。
  3. 主要应用xgb、lgb、catboost，以及pandas、numpy、matplotlib、seabon、sklearn、keras等等数据挖掘常用库或者框架来进行数据挖掘任务。
  4. 通过EDA来挖掘数据的联系和自我熟悉数据

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import pandas as pd

# 1) 载入训练集和测试集
Train_data = pd.read_csv('./datalab/used_car_train_20200313.csv',sep=(' '))
Test_data = pd.read_csv('./datalab/used_car_testA_20200313.csv',sep=(' '))

print(Train_data.shape) # 返回行,列数
print(Test_data.shape)
out_put = Train_data.head(4) # 返回前四行字段数据
print(out_put)

# 2)分类指标评价计算

## accuracy
from sklearn.metrics import accuracy_score
y_pred = [0, 1, 0, 1] # 预测标签
y_true = [0, 1, 1, 1] # 正确标签
print('ACC:',accuracy_score(y_true, y_pred)) # 返回正确样本所占比例（float）


"""
TP：真正例：即将正样本预测为正样本
TN：真反例：即将负样本预测为负样本
FP：假正例：将负样本预测为了正样本
FN：假反例：将正样本预测为了负样本
"""
## Percision,Recall,F1-score
from sklearn import metrics
y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]
print('Precision',metrics.precision_score(y_true, y_pred)) # 返回 TP / (TP + FP)
print('Recall',metrics.recall_score(y_true, y_pred)) # 返回 TP / (TP + FN)
print('F1-score:',metrics.f1_score(y_true, y_pred)) # 返回 2*(P*R)/(P+R)

## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1]) # True labels or binary label indicators
y_scores = np.array([0.1, 0.4, 0.35, 0.8]) # Target scores
print('AUC socre:',roc_auc_score(y_true, y_scores))

# coding=utf-8
# import numpy as np
# from sklearn import metrics

# MAPE需要自己实现
def mape(y_true, y_pred):
    return np.mean(np.abs((y_pred - y_true) / y_true))

y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])

# MSE
print('MSE:',metrics.mean_squared_error(y_true, y_pred))
# RMSE
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
# MAE
print('MAE:',metrics.mean_absolute_error(y_true, y_pred))
# MAPE
print('MAPE:',mape(y_true, y_pred))

## R2-score
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print('R2-score:',r2_score(y_true, y_pred))